O namoro e o domínio das funções

As funções são casos particulares de relação entre os elementos de dois conjuntos, A e B, por exemplo, em que cada elemento de A se relaciona com um e somente um elemento de B.

O estudo delas nos ajuda a compreender melhor a forma como se dão esses relacionamentos e, na mesma linha, ampliam as nossas possibilidades de compreensão do mundo interligado em redes em que vivemos.

Para entender melhor esse conceito, costumo brincar com os alunos dizendo o seguinte: Na função Namoro entre os Homens de um conjunto A e as Mulheres de um conjunto B:
a) Todo homem deve ter uma e somente uma namorada. O homem não pode ficar sem namorar, mas também não pode ter mais de uma namorada;

b) Todos os homens de A podem namorar a mesma mulher, o que, inversamente falando, quer dizer que uma mulher dessa relação pode ter todos os homens que quiserem namorar com ela.

No entanto, quem escolhe com quem vai namorar nessa relação Homens x Mulheres, são os homens. São os elementos do primeiro conjunto que DOMINAM a relação.

Domínio de uma função, portanto, é o conjunto formado pelos elementos independentes de uma relação/função, que controlam essa relação e que determinam quem se relacionará com quem. Os elementos do domínio da função são os pontos de partida da relação.

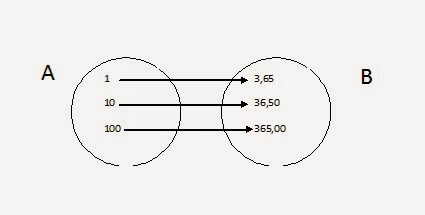
Se considerarmos a relação representada em um diagrama, podemos dizer que o Domínio da Função, ou seja, D(f) é o conjunto de partida das flechas. No exemplo acima, D(f) = A = {1, 10, 100}.

Já o conjunto de chegada das flechas, aquele que contém os elementos que se relacionarão com os elementos do Domínio da Função é chamado de CONTRADOMÍNIO, CD(F). No exemplo acima, o CD(f) = B. O contradomínio sempre será o conjunto B, incluindo todos os seus elementos, mesmo aqueles que não estiverem relacionados com elementos de A.

Finalmente nós temos o conjunto IMAGEM de uma função de A em B, o qual é formado por todos os elementos de B, ou seja, do segundo conjunto da relação e que se relacionam com elementos de A. Somente são imagens dos elementos de A, aqueles elementos de B que se relacionam com eles. No exemplo acima, a imagem de 1 é 3,65; a imagem de 10 é 36,50 e a imagem de 100 é 365,00. O conjunto imagem dessa função é igual ao conjunto contradomínio, mas nem sempre é assim. 

O conjunto IMAGEM de uma função sempre estará contido no conjunto CONTRADOMÍNIO  dessa mesma função, podendo ser menor ou igual ao contradomínio.

Os elementos de A e B que se relacionam biunivocamente, ou seja, um a um, formam grupos pares de elementos, que designamos por PARES ORDENADOS (x, y), onde o elemento x pertence ao domínio da função, ao primeiro conjunto da relação e o elemento y pertence à imagem da função, ou seja, ao segundo conjunto da relação.

Cada par ordenado (x, y) corresponde a um ponto geométrico, o qual pode ser representado no Plano Cartesiano.

O Plano Cartesiano é formado por duas retas ou eixos perpendiculares x e y, sendo que o eixo x é chamado de eixo das abscissas e o eixo y é chamado de eixo das ordenadas. Os valores de x são as abscissas e são marcados nesse eixo; os valores de y são as ordenadas e são marcados no eixo das ordenadas.

Após marcar os pontos de uma relação/função no plano cartesiano, podemos ligá-los, formando um gráfico.

Cada função tem um tipo de gráfico. 

Função do 1º grau: o gráfico é uma reta

Por exemplo, o gráfico de uma função do 1º grau é uma RETA. 

Função quadrática: o gráfico é uma parábola

 O gráfico de uma função quadrática, ou do 2º grau é uma parábola.

No início do estudo das funções, normalmente, os valores de x (a variável determinante) costumam ser dados previamente. Na continuidade dos estudos, isso nem sempre acontece.

Quando os valores de x não são dados no exercício, isso quer dizer que x poderá assumir qualquer valor real em que for possível realizar os cálculos na lei de formação para determinar o valor correspondente de y, ou seja, a imagem do valor x considerado.

Lei de formação é a fórmula ou regra geral que define uma relação/função. No exemplo já estudado correspondente ao abastecimento de um carro em que o D(f) = {1, 10, 100} e a Im (f) = {3,65; 36,50; 365,00}, é possível perceber que a lei de formação que define essa função é f(x) = 3,65x ou y = 3,65 x, onde 3,65 é o valor de 1 litro de gasolina e x é a quantidade de litros de gasolina abastecido.

Vemos que, alterando o valor de x, consequentemente alteramos o valor de y, quando fazemos a substituição de x pelo valor atribuído.

Então, como dizíamos, quando o valor do Domínio de uma função não for dado e lhe for solicitado determinar o domínio dessa função, o que você fará será a verificação de quais valores poderão ser atribuídos ao x, de forma que, ao substituir tais valores na lei de formação dado, sejam possíveis realizar os cálculos dentro do conjunto dos números reais, se for uma função de R em R, ou seja, com ponto de partida e de chegada, no conjunto dos números reais R.

Exemplificando. Se tivermos que calcular o domínio das funções abaixo, o que faremos será analisar as possíveis restrições de valores para x.

Vejamos:
a) No exemplo 1, não nenhuma restrição. Nós podemos colocar o valor que quisermos no lugar de x que o cálculo será possível em R;

b) Já no exemplo 2, não é assim. O valor de x está dentro do radical. ele faz parte do radicando. Nós já sabemos de estudos anteriores que "não existe raiz quadrada de número negativo em R". Logo, esse radicando não poderá ser um número negativo. 
Assim, x + 1 deve ser maior ou igual a zero. E x terá que ser maior ou igual a -1 Um negativo).

c) No exemplo 3, o x aparece no denominador da fração. Sabemos que em R, "não existe divisão por zero". Portanto, o denominador x+ 1 deve ser diferente de zero e assim, x deve ser diferente de -1.

d) No exemplo 4, x aparece dentro do radical e no denominador. Então, nesse caso temos duas restrições. O denominador não pode ser negativo e nem tampouco pode ser igual a zero.

Vejamos como ficou o nosso estudo do domínio dessas funções:

Então,por enquanto, é isso. Posteriormente, falaremos mais sobre esse assunto.