Um Plano de Curso de Matemática para o
Ensino Médio/2015
Prof. Izaias Resplandes de Sousa
Carga horária: 3 aulas semanais.
Introdução
São eixos cognitivos para o Ensino
Médio:
I- Dominar a norma culta da Língua
Portuguesa e fazer uso das linguagens matemática, artística e científica.
II- Construir e aplicar conceitos das
várias áreas do conhecimento para a compreensão de fenômenos naturais, de
processos histórico-geográficos, da produção tecnológica e das manifestações
artísticas.
III- Selecionar, organizar, relacionar,
interpretar dados e informações representadas de diferentes formas, para tomar
decisões e enfrentar situações-problema.
IV- Relacionar informações,
representadas em diferentes formas, e conhecimentos disponíveis em situações
concretas, para construir argumentação consistente.
V- Recorrer aos conhecimentos
desenvolvidos para elaboração de propostas de intervenção solidária na
realidade, respeitando os valores humanos e considerando a diversidade
sociocultural.
De
acordo com os PCN+, a área de Ciências da Natureza, Matemática e suas
Tecnologias elegeu três grandes competências como metas a serem perseguidas:
1) Representação
e comunicação: leitura, transmissão de idéias, interpretação e
produção de textos nas diversas formas características da área.
Algumas
habilidades referentes a esta competência são:
• Ler e interpretar dados apresentados em
tabelas, gráficos, diagramas, fórmulas, equações, ou representações
geométricas;
• Traduzir informações de uma dessas
formas de apresentação para outra; utilizar essas formas de apresentação de
informações selecionando, em cada caso, as mais adequadas;
• Ler e interpretar diferentes tipos de
textos com informações apresentadas na forma de linguagem matemática como, por
exemplo, artigos de conteúdo econômico, que aparecem em jornais e revistas,
social ou cultural, em propagandas de promoções e vendas, apresentados em
folhetos ou na mídia;
• Expressar-se com clareza sobre temas
matemáticos oralmente ou por escrito.
2) Investigação e compreensão: capacidade
de enfrentar desafios e resolução de situações problema, utilizando-se de
conceitos e procedimentos peculiares (experimentação, abstração, modelagem).
Algumas
habilidades referentes a esta competência são:
* Identificar os dados relevantes numa
situação-problema para buscar possíveis resoluções;
* Elaborar estratégias para enfrentar e
resolver uma dada situação-problema;
* Identificar regularidade em dadas
situações; Fazer estimativas;
* Interpretar, fazer uso e elaborar
modelos e representações matemáticas para analisar situações;
* Reconhecer relações entre a
matemática e outras áreas do conhecimento.
3) Contextualização:
no âmbito histórico ou sócio-cultural, na forma de análise crítica das idéias e
dos recursos da área, para questionar, modificar ou resolver problemas
propostos.
Algumas
habilidades referentes a esta competência são:
• Compreender a construção do conhecimento
matemático como um processo histórico, em estreita relação com as condições
sociais, políticas e econômicas de uma determinada época;
• Compreender a responsabilidade social
associada à aquisição e ao uso do conhecimento matemático, sentindo-se mobilizado
para diferentes ações que envolvam seu interesse como cidadão ou de sua
comunidade;
• Utilizar as ferramentas matemáticas
para analisar situações de seu entorno real e propor soluções; etc.
Conteúdos Programáticos:
1º ano:
1º bimestre
Conteúdos.
Revisão de Produtos notáveis,
fatoração, equações do 1º e 2º graus.
Objetivo específico:
-
Recordar conhecimentos considerados como pré-requisitos necessários para os
estudos de matemática no ensino médio.
-
Reconhecer e determinar o quadrado da soma de dois termos;
-
Reconhecer e determinar o quadrado da diferença entre dois termos;
-
Reconhecer e determinar o produto da soma pela diferença de dois termos;
-
Resolver situações-problema envolvendo produtos notáveis;
-
Conhecer e aplicar os principais casos de fatoração
-
Reconhecer uma equação do 1º grau e determine suas raízes;
-
Interpretar e representar equações do 1º grau algébrica e geometricamente;
-
Resolver situações-problema envolvendo equações do 1º grau;
-
Reconhecer uma equação do 2º grau e determine suas raízes;
-
Interpretar e representar equações do 2º grau algébrica e geometricamente;
-
Resolver situações-problema envolvendo equações do 2º grau;
Conteúdos.
Plano
cartesiano: teoria e aplicação.
Função:
generalidades: conceito, notação, representação, domínio, contradomínio,
imagem, gráfico. Função do 1º grau: Definição; Tipos
(constante, afim, linear), coeficientes angular e linear, zero da função,
crescimento e decrescimento, estudo do sinal, construção, leitura e análise de
gráficos.
Objetivos
específicos:
- Identificar e construir o plano
cartesiano.
- Representar pontos no plano
cartesiano.
- Formalizar o conceito de função.
- Reconhecer funções em situações do
cotidiano.
- Reconhecer domínio, imagem e
contradomínio da função.
- Determinar a imagem pela lei y =
f(x);
- Estudar o sinal da função.
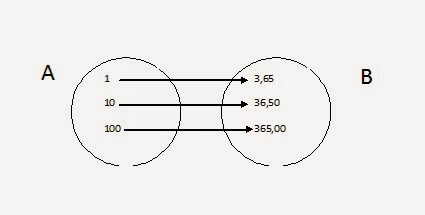
- Representar uma função por meio de
diagramas.
- Representar uma função por meio de
gráficos.
- Reconhecer uma função pela análise
gráfica.
- Reconhecer o gráfico das funções
afim, linear e constante.
- Construir o gráfico das funções afim,
linear e constante.
- Determinar a lei de associação, com
base no gráfico das funções afim, linear e constante.
- Estudar os sinais dos períodos das
funções afim e linear
2º
bimestre.
Conteúdos.
Função quadrática: definição, zero da
função; Vértice da parábola; Imagem; Construção do gráfico
Objetivos
específicos:
- Identificar a lei de formação de uma função
quadrática a partir de sua representação algébrica e/ou gráfica;
- Reconhecer uma função quadrática nas suas
representações algébrica e gráfica;
-
Calcular as raízes de uma função quadrática;
-
Identificar o ponto de máximo e de mínimo de uma função quadrática;
-
Definir o vértice da parábola na função quadrática
-
Construir o gráfico da função quadrática
-
Determinar o número de raízes de uma função quadrática por meio da análise de
sua representação gráfica (concavidade da parábola);
-
Identificar uma função quadrática em situações descritas em um texto,
representando-a algébrica e/ou graficamente;
-
Resolver situações-problema que envolvam a função quadrática;
3º bimestre.
Conteúdos.
Sequências
Numéricas. Termo geral. Progressão Aritimética: definição, classificação, termo
geral, Resolução de problemas, Soma dos termos da PA. Progressão Geométrica:
definição, classificação, termo geral, Resolução de problemas, Soma dos termos
da PG.
Objetivos específicos:
-
Diferenciar os conceitos de sequência e conjunto.
-
Identificar a lei de formação de Progressões Aritméticas;
-
Determinar os termos de uma sequência, a partir de sua lei de formação.
-
Definir uma progressão aritmética.
-
Classificar uma progressão aritmética como crescente, decrescente ou constante.
- Compreender
e operar com a fórmula do termo geral de uma Progressão Aritmética;
-
Determinar, utilizando a lei de formação, um termo qualquer de uma progressão
aritmética.
-
Representar genericamente uma PA.
-
Calcular a soma dos n primeiros termos de uma PA.
-
Compreender e operar com a fórmula da soma dos termos de uma Progressão
Aritmética;
-
Definir uma progressão geométrica (PG).
-
Identificar a lei de formação de Progressões Geométricas;
-
Identificar a razão de uma Progressão
Geométrica;
-
Classificar uma PG como crescente, decrescente, constante, alternante ou quase
nula.
-
Determinar, utilizando a lei de formação, um termo qualquer de uma PG.
- Compreender e operar com a fórmula da soma dos
termos de uma Progressão Geométrica;
-
Representar genericamente uma PG.
-
Calcular a soma dos n primeiros termos de uma PG.
- Identificar uma Progressão Geométrica em
situações descritas em um texto, representando-a em linguagem algébrica;
-
Resolver situações-problema envolvendo
Progressões Aritméticas e/ou Geométricas;
4º bimestre
Conteúdos.
Triângulo
retângulo. Relações métricas. Trigonometria no triângulo retângulo. Seno,
Cosseno e Tangente de um ângulo agudo.
Objetivos específicos:
-
Identificar as relações métricas no triângulo retângulo e aplicá-las na resolução
de problemas variados.
- Calcular
a medida de um lado de um triângulo, a partir das medidas de outro lado e de um
ângulo agudo desse triângulo.
- Resolver situações-problema envolvendo
as relações métricas no triângulo retângulo;
-
Compreender os conceitos e calcular os valores aproximados do seno, cosseno e
tangente de um ângulo agudo de um triângulo retângulo.
- Utilizar as razões trigonométricas no
triângulo retângulo para obter relações entre ângulos e lados na determinação
de suas medidas;
-
Resolver situações-problema envolvendo
as relações trigonométricas no triângulo retângulo;
2º ano:
1º bimestre.
Conteúdos:
Matrizes: introdução, representação,
tipos de matrizes, Igualdade de matrizes. Adição, subtração e multiplicação de
matrizes.
Objetivos específicos:
-
Conceituar e interpretar matrizes e suas operações;
-
Reconhecer, interpretar e transcrever dados em linguagem matricial;
-Reconhecer
uma matriz e saber utilizar suas operações.
-
Classificar as matrizes em identidade, nula, transposta, oposta, linha, coluna,
quadrada.
- Resolver
situações-problema envolvendo a igualdade e operações de adição, subtração e
multiplicação de matrizes;
2º
bimestre.
Conteúdos:
Determinantes: conceito; Cálculo de
determinantes pela Regra de Sarrus, Regra de Cramer e Teorema de Laplace.
Objetivos
específicos:
- Calcular o determinante de matrizes
de ordem 1, 2 e 3
- Conhecer e aplicar a Regra de Sarrus,
a Regra de Cramer e o Teorema de Laplace no cálculo de determinantes.
3º
bimestre.
Conteúdos:
Sistemas Lineares: métodos de
resolução: adição, substituição, escalonamento. Discussão de um sistema.
Objetivos específicos:
-
Reconhecer uma equação linear.
-
Resolver problemas que envolvam sistemas de equações lineares.
-
Reconhecer uma equação linear.
-
Determinar soluções de uma equação linear possível.
-
Classificar uma equação linear em possível ou
impossível.
-
Classificar os sistemas lineares em SPD, SPI e SI
-
Resolver sistemas lineares pelos métodos da adição e substituição
4º
bimestre.
Conteúdos:
Análise combinatória: Princípio
fundamental da contagem. Fatorial de um número natural. Agrupamentos simples.
Permutações. Arranjos. Combinações. Permutações de elementos repetidos.
Objetivos específicos:
-
Reconhecer situações em que a contagem dos resultados possíveis é parte da
resolução do problema.
-
Definir o que é Análise combinatória.
-
Aplicar o princípio fundamental de contagem.
-
Calcular o fatorial de um número natural.
-
Resolver equações envolvendo fatoriais
-
Classificar agrupamentos simples como arranjos ou combinações.
-
Reconhecer um arranjo simples.
-
Construir os arranjos simples formados por p elementos escolhidos entre n
elementos distintos.
-
Calcular o número de arranjos simples de n elementos tomados p a p.
-
Reconhecer uma permutação simples.
-
Construir permutações de n elementos distintos.
-
Calcular o número de permutações simples e de permutações com elementos
repetidos.
-
Reconhecer uma combinação simples.
-
Construir as combinações simples formadas por p elementos escolhidos entre n
elementos distintos.
-
Relacionar os números Cn,p e Anp.
Conteúdos:
Probabilidade: espaço amostral, evento,
freqüência relativa e probabilidade. Aplicações.
Objetivos específicos:
-
Determinar o espaço amostral de um experimento aleatório.
-
Determinar o número de elementos de um espaço amostral.
-
Definir evento de um espaço amostral.
-
Calcular a probabilidade de ocorrer um evento em um espaço amostral.
-
Reconhecer eventos complementares.
-
Aplicar as propriedades das probabilidades.
-
Resolver problemas de probabilidade
3º ano:
1º
bimestre.
Conteúdos:
Atividades de revisão de funções:
domínio, imagem, valor numérico, gráficos,
diagramas, leis de formação, tipos de função: constante, 1º grau, 2º
grau, crescente, decrescente, quadrática Subconjuntos dos Reais. Linguagem
matemática
Objetivos
específicos:
- Rever conteúdos do 1º ano médio,
considerados pré-requisitos para o prosseguimento dos estudos.
Conteúdos:
Estatística: tabelas de freqüência,
representações gráficas, Medidas de tendência central. Medidas de dispersão.
Objetivos
específicos:
- Conceituar Estatística
- Conceituar população, amostra,
frequência e frequência relativa.
- Separar uma amostra de números em
classes.
- Construir tabelas de distribuição
de frequência.
- Analisar, interpretar e organizar
dados e informações de pesquisas estatísticas em gráficos e tabelas
- Representar uma distribuição de
frequência em gráfico de linha, gráfi co de barras (horizontais e verticais) e
gráfico de setores.
- Construir e interpretar histogramas
de uma distribuição de frequência de classes não unitárias.
-
Conceituar média aritmética.
-
Conceituar média ponderada.
-
Conceituar moda e mediana.
-
Conceituar as medidas de dispersão: Variância e Desvio Padrão
-
Calcular a Variância
-
Calcular o desvio padrão
-
Analisar e interpretar resultados de pesquisas estatísticas realizadas por
amostragem;
-
Identificar e interpretar dados e informações estatísticas por meio de sua
representação gráfica;
-
Resolver situações-problema envolvendo pesquisas estatísticas.
2º bimestre.
Conteúdos:
Números
complexos: introdução. Forma algébrica de z. Conjugado. Número complexo.
Operações em z.
Objetivos
específicos:
- Identificar
os diferentes conjuntos numéricos e as propriedades inerentes a cada um deles;
- Introduzir a noção de números
complexos.
- Identificar a unidade imaginária (i)
como elemento do conjunto dos números complexos
- Conceituar número complexo e
representá-lo na forma algébrica e gráfica.
- Operar com a forma algébrica dos
números complexos
- Calcular potências de expoente
inteiro de i e de números complexos na forma a + bi, sendo a e b números reais.
- Resolver situações-problema
envolvendo o cálculo de equações cujas raízes não são reais;
3º
bimestre.
Conteúdos:
Geometria Analítica: Ponto: distância
entre dois pontos. Ponto médio de um segmento. Mediana e baricentro. Condição
de alinhamento de 3 pontos. Resolução de problemas.
Objetivos
específicos:
- Conhecer a origem do sistema de
coordenadas cartesianas.
- Calcular a distância entre dois
pontos.
- Obter o ponto médio de um segmento de
reta.
- Identificar, graficamente, a
inclinação de uma reta no plano cartesiano.
- Calcular o coeficiente angular de uma
reta não vertical, conhecendo sua inclinação ou as coordenadas de dois de seus
pontos.
- Verificar se três pontos do plano
cartesiano são ou não colineares.
4º
bimestre.
Conteúdos:
A reta: equação geral da reta.
Intersecção de retas. Inclinação de uma reta (coeficiente angular). Equação
reduzida. Paralelismo. Perpendicularidade.
Objetivos específicos:
-
Representar uma reta do plano cartesiano por meio de uma equação geral.
-
Determinar os pontos de intersecção de duas retas concorrentes.
-
Expressar a equação geral de uma reta não vertical na forma reduzida,
destacando os coeficientes angular e linear.
-
Reconhecer a posição relativa de duas retas não verticais a partir de seus
coeficientes angulares
Metodologia:
Aulas expositivas e trabalhos
individuais e em grupo. Excepcionalmente, conforme a disponibilidade será
utilizada os recursos da mídia e informática.
Avaliação: Conforme as normas da escola.