CRITÉRIOS DE AVALIAÇÃO DO ENEM EM MATEMÁTICA

Conheça aqui o que é cobrado na avaliação do ENEM, em Matemática

EIXOS COGNITIVOS (comuns a todas as áreas de conhecimento)

I. Dominar linguagens (DL): dominar a norma culta da Língua Portuguesa e fazer uso das linguagens matemática, artística e científica e das línguas espanhola e inglesa.

II. Compreender fenômenos (CF): construir e aplicar conceitos das várias áreas do conhecimento para a compreensão de fenômenos naturais, de processos histórico-geográficos, da produção tecnológica e das manifestações artísticas.

III. Enfrentar situações-problema (SP): selecionar, organizar, relacionar, interpretar dados e informações representados de diferentes formas, para tomar decisões e enfrentar situações-problema.

IV. Construir argumentação (CA): relacionar informações, representadas em diferentes formas, e conhecimentos disponíveis em situações concretas, para construir argumentação consistente.

V. Elaborar propostas (EP): recorrer aos conhecimentos desenvolvidos na escola para elaboração de propostas de intervenção solidária na realidade, respeitando os valores humanos e considerando a diversidade sociocultural.

Matriz de Referência de Matemática e suas Tecnologias

Competência de área 1 - Construir significados para os números naturais, inteiros, racionais e reais. H1 - Reconhecer, no contexto social, diferentes significados e representações dos números e operações - naturais, inteiros, racionais ou reais.
H2 - Identificar padrões numéricos ou princípios de contagem.
H3 - Resolver situação-problema envolvendo conhecimentos numéricos.
H4 - Avaliar a razoabilidade de um resultado numérico na construção de argumentos sobre afirmações quantitativas.
H5 - Avaliar propostas de intervenção na realidade utilizando conhecimentos numéricos.

Competência de área 2 - Utilizar o conhecimento geométrico para realizar a leitura e a representação da realidade e agir sobre ela.
H6 - Interpretar a localização e a movimentação de pessoas/objetos no espaço tridimensional e sua representação no espaço bidimensional.
H7 - Identificar características de figuras planas ou espaciais.
H8 - Resolver situação-problema que envolva conhecimentos geométricos de espaço e forma.
H9 - Utilizar conhecimentos geométricos de espaço e forma na seleção de argumentos propostos como solução de problemas do cotidiano.

Competência de área 3 - Construir noções de grandezas e medidas para a compreensão da realidade e a solução de problemas do cotidiano.
H10 - Identificar relações entre grandezas e unidades de medida.
H11 - Utilizar a noção de escalas na leitura de representação de situação do cotidiano.
H12 - Resolver situação-problema que envolva medidas de grandezas.
H13 - Avaliar o resultado de uma medição na construção de um argumento consistente.
H14 - Avaliar proposta de intervenção na realidade utilizando conhecimentos geométricos relacionados a grandezas e medidas.

 Competência de área 4 - Construir noções de variação de grandezas para a compreensão da realidade e a solução de problemas do cotidiano.
H15 - Identificar a relação de dependência entre grandezas.
H16 - Resolver situação-problema envolvendo a variação de grandezas, direta ou inversamente proporcionais.
H17 - Analisar informações envolvendo a variação de grandezas como recurso para a construção de argumentação.
H18 - Avaliar propostas de intervenção na realidade envolvendo variação de grandezas.

Competência de área 5 - Modelar e resolver problemas que envolvem variáveis socioeconômicas ou técnico-científicas, usando representações algébricas.
H19 - Identificar representações algébricas que expressem a relação entre grandezas.
H20 - Interpretar gráfico cartesiano que represente relações entre grandezas.
H21 - Resolver situação-problema cuja modelagem envolva conhecimentos algébricos.
H22 - Utilizar conhecimentos algébricos/geométricos como recurso para a construção de argumentação.
H23 - Avaliar propostas de intervenção na realidade utilizando conhecimentos algébricos.

Competência de área 6 - Interpretar informações de natureza científica e social obtidas da leitura de gráficos e tabelas, realizando previsão de tendência, extrapolação, interpolação e interpretação.
H24 - Utilizar informações expressas em gráficos ou tabelas para fazer inferências.
H25 - Resolver problema com dados apresentados em tabelas ou gráficos.
H26 - Analisar informações expressas em gráficos ou tabelas como recurso para a construção de argumentos.

 Competência de área 7 - Compreender o caráter aleatório e não-determinístico dos fenômenos naturais e sociais e utilizar instrumentos adequados para medidas, determinação de amostras e cálculos de probabilidade para interpretar informações de variáveis apresentadas em uma distribuição estatística.
H27 - Calcular medidas de tendência central ou de dispersão de um conjunto de dados expressos em uma tabela de freqüências de dados agrupados (não em classes) ou em gráficos.
H28 - Resolver situação-problema que envolva conhecimentos de estatística e probabilidade.
H29 - Utilizar conhecimentos de estatística e probabilidade como recurso para a construção de argumentação.
H30 - Avaliar propostas de intervenção na realidade utilizando conhecimentos de estatística e probabilidade.

Atividades de Geometria

ESCOLA ESTADUAL PROFª JURACY MACÊDO

AVALIAÇÃO DE MATEMÁTICA – 9º ANO MATUTINO

ALUNO (A): ________________________________________________

Marque a alternativa correspondente à solução de cada questão:

01) Analise se as afirmações referentes à Geometria são verdadeiras ou falsas:

I. Os pontos são indicados por letras maiúsculas e as retas por letras minúsculas do alfabeto latino (nosso alfabeto).

II. Reta e Semirreta são figuras infinitas, mas enquanto a reta não tem nem começo e nem fim, a semirreta não tem apenas fim.

III. Um segmento de reta é uma parte da reta compreendida entre dois de seus pontos.

Agora responda:

a) Todas as alternativas estão erradas.

b) Todas as alternativas estão corretas.

c) Somente a alternativa I está correta.

d) Somente as alternativas I e II estão corretas.

e) Somente as alternativas II e III estão corretas.

02) Analise se as afirmações referentes aos são verdadeiras ou falsas:

I. Ângulo é a região do plano delimitada por duas semirretas de mesma origem.

II. O Vértice de um ângulo é o ponto de origem das duas semirretas que  formam esse ângulo.

III. Um ângulo é medido em graus e o instrumento adequado para medi-lo é a régua.

Agora responda:

a) Todas as alternativas estão erradas.

b) Todas as alternativas estão corretas.

c) Somente a alternativa I está correta.

d) Somente as alternativas I e II estão corretas.

e) Somente as alternativas II e III estão corretas.

03) Analise se as afirmações referentes ao Grau são verdadeiras ou falsas:

I. 1° é igual a 60”.

II. 1° é igual a 60’.

III. 1’ é igual a 60”.

Agora responda:

a) Todas as alternativas estão erradas.

b) Todas as alternativas estão corretas.

c) Somente a alternativa I está correta.

d) Somente as alternativas I e II estão corretas.

e) Somente as alternativas II e III estão corretas.

04) Dois ângulos são suplementares quando:

a) a soma de suas medidas for igual a 90°.

b) a soma de suas medidas for igual a 360º.

c) a soma de suas medidas for igual a 90°

d) a diferença entre eles for um ângulo reto.

e) a diferença entre eles for um ângulo obtuso.

05) Um polígono convexo com 20 lados é chamado de:

a) Icosagono         b) Dodecágono        c) Pentadecágono

d) Undecágono     e) Octodecágono.

06) Diagonal é o segmento de reta determinado por dois pontos não-consecutivos de um polígono convexo. O eneágono tem:

a) 9 diagonais   b) 18 diagonais       c) 24 diagonais   

d) 27 diagonais       e) 54 diagonais.

07) O perímetro é a soma de todos os lados se um polígono convexo. A sala de aula tem 6 metros de largura por 8 metros de comprimento. Logo, a medida de seu perímetro é:

a) 14 metros     b) 28 metros      c) 48 metros       

d) 14 metros quadrados       e) 48 metros quadrados.

08) O complemento de um ângulo é o que falta nele para que tenha a medida de 90 graus. Assim, o complemento de 35°14’20” é:

a) 54°45’40”     b) 55°45’40”      c) 45°45’40”

d) 54°40”45”       e) 55°

09) A medida de dois ângulo complementares vale (2â + 10°) e (â + 50°). Desse modo, a medida de cada ângulo é, respectivamente:

a) 60° e 30°       b) 75° e 15°       c) 30° e 60°  

d) 40º e 50º       e) 10º 80º

10) A metade do ângulo de medida 49°2’10” é:

a) 24° 31’5”      b) 25º 31’5”     c) 23°31’5”

d) 24 graus     e) 24 graus e meio

O namoro e o domínio das funções

As funções são casos particulares de relação entre os elementos de dois conjuntos, A e B, por exemplo, em que cada elemento de A se relaciona com um e somente um elemento de B.

O estudo delas nos ajuda a compreender melhor a forma como se dão esses relacionamentos e, na mesma linha, ampliam as nossas possibilidades de compreensão do mundo interligado em redes em que vivemos.

Para entender melhor esse conceito, costumo brincar com os alunos dizendo o seguinte: Na função Namoro entre os Homens de um conjunto A e as Mulheres de um conjunto B:
a) Todo homem deve ter uma e somente uma namorada. O homem não pode ficar sem namorar, mas também não pode ter mais de uma namorada;

b) Todos os homens de A podem namorar a mesma mulher, o que, inversamente falando, quer dizer que uma mulher dessa relação pode ter todos os homens que quiserem namorar com ela.

No entanto, quem escolhe com quem vai namorar nessa relação Homens x Mulheres, são os homens. São os elementos do primeiro conjunto que DOMINAM a relação.

Domínio de uma função, portanto, é o conjunto formado pelos elementos independentes de uma relação/função, que controlam essa relação e que determinam quem se relacionará com quem. Os elementos do domínio da função são os pontos de partida da relação.

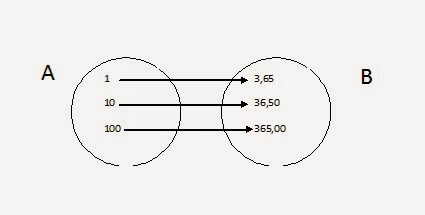
Se considerarmos a relação representada em um diagrama, podemos dizer que o Domínio da Função, ou seja, D(f) é o conjunto de partida das flechas. No exemplo acima, D(f) = A = {1, 10, 100}.

Já o conjunto de chegada das flechas, aquele que contém os elementos que se relacionarão com os elementos do Domínio da Função é chamado de CONTRADOMÍNIO, CD(F). No exemplo acima, o CD(f) = B. O contradomínio sempre será o conjunto B, incluindo todos os seus elementos, mesmo aqueles que não estiverem relacionados com elementos de A.

Finalmente nós temos o conjunto IMAGEM de uma função de A em B, o qual é formado por todos os elementos de B, ou seja, do segundo conjunto da relação e que se relacionam com elementos de A. Somente são imagens dos elementos de A, aqueles elementos de B que se relacionam com eles. No exemplo acima, a imagem de 1 é 3,65; a imagem de 10 é 36,50 e a imagem de 100 é 365,00. O conjunto imagem dessa função é igual ao conjunto contradomínio, mas nem sempre é assim. 

O conjunto IMAGEM de uma função sempre estará contido no conjunto CONTRADOMÍNIO  dessa mesma função, podendo ser menor ou igual ao contradomínio.

Os elementos de A e B que se relacionam biunivocamente, ou seja, um a um, formam grupos pares de elementos, que designamos por PARES ORDENADOS (x, y), onde o elemento x pertence ao domínio da função, ao primeiro conjunto da relação e o elemento y pertence à imagem da função, ou seja, ao segundo conjunto da relação.

Cada par ordenado (x, y) corresponde a um ponto geométrico, o qual pode ser representado no Plano Cartesiano.

O Plano Cartesiano é formado por duas retas ou eixos perpendiculares x e y, sendo que o eixo x é chamado de eixo das abscissas e o eixo y é chamado de eixo das ordenadas. Os valores de x são as abscissas e são marcados nesse eixo; os valores de y são as ordenadas e são marcados no eixo das ordenadas.

Após marcar os pontos de uma relação/função no plano cartesiano, podemos ligá-los, formando um gráfico.

Cada função tem um tipo de gráfico. 

Função do 1º grau: o gráfico é uma reta

Por exemplo, o gráfico de uma função do 1º grau é uma RETA. 

Função quadrática: o gráfico é uma parábola

 O gráfico de uma função quadrática, ou do 2º grau é uma parábola.

No início do estudo das funções, normalmente, os valores de x (a variável determinante) costumam ser dados previamente. Na continuidade dos estudos, isso nem sempre acontece.

Quando os valores de x não são dados no exercício, isso quer dizer que x poderá assumir qualquer valor real em que for possível realizar os cálculos na lei de formação para determinar o valor correspondente de y, ou seja, a imagem do valor x considerado.

Lei de formação é a fórmula ou regra geral que define uma relação/função. No exemplo já estudado correspondente ao abastecimento de um carro em que o D(f) = {1, 10, 100} e a Im (f) = {3,65; 36,50; 365,00}, é possível perceber que a lei de formação que define essa função é f(x) = 3,65x ou y = 3,65 x, onde 3,65 é o valor de 1 litro de gasolina e x é a quantidade de litros de gasolina abastecido.

Vemos que, alterando o valor de x, consequentemente alteramos o valor de y, quando fazemos a substituição de x pelo valor atribuído.

Então, como dizíamos, quando o valor do Domínio de uma função não for dado e lhe for solicitado determinar o domínio dessa função, o que você fará será a verificação de quais valores poderão ser atribuídos ao x, de forma que, ao substituir tais valores na lei de formação dado, sejam possíveis realizar os cálculos dentro do conjunto dos números reais, se for uma função de R em R, ou seja, com ponto de partida e de chegada, no conjunto dos números reais R.

Exemplificando. Se tivermos que calcular o domínio das funções abaixo, o que faremos será analisar as possíveis restrições de valores para x.

Vejamos:
a) No exemplo 1, não nenhuma restrição. Nós podemos colocar o valor que quisermos no lugar de x que o cálculo será possível em R;

b) Já no exemplo 2, não é assim. O valor de x está dentro do radical. ele faz parte do radicando. Nós já sabemos de estudos anteriores que "não existe raiz quadrada de número negativo em R". Logo, esse radicando não poderá ser um número negativo. 
Assim, x + 1 deve ser maior ou igual a zero. E x terá que ser maior ou igual a -1 Um negativo).

c) No exemplo 3, o x aparece no denominador da fração. Sabemos que em R, "não existe divisão por zero". Portanto, o denominador x+ 1 deve ser diferente de zero e assim, x deve ser diferente de -1.

d) No exemplo 4, x aparece dentro do radical e no denominador. Então, nesse caso temos duas restrições. O denominador não pode ser negativo e nem tampouco pode ser igual a zero.

Vejamos como ficou o nosso estudo do domínio dessas funções:

Então,por enquanto, é isso. Posteriormente, falaremos mais sobre esse assunto.

Por que estudar Matemática?

A razão e os porquês de estudarmos isso ou aquilo está no cerne do sucesso ou do fracasso escolar. "Aprende-se o que interessa", já recordamos de Amaral Fontoura. Portanto, o interesse é uma das condições da aprendizagem. Para aprender é preciso querer aprender.

Você quer mesmo aprender Matemática ou qualquer outra coisa na vida?

O querer está ligado à satisfação de uma necessidade. Qualquer que seja, mas sempre haverá uma necessidade a ser satisfeita com a colocação em prática do nosso ato de querer.

Sinteticamente, podemos dizer que a Matemática fora criada para ajudar o homem a contar o seu patrimônio, as coisas que possuía, ou ainda aquelas que desejava possuir.

Quantas vacas eu tenho? Quantos reais eu possuo? 

Se eu sei contar eu posso medir o poder que eu possuo e posso me esforçar para mantê-lo ou para aumentá-lo e também terei consciência se ele está diminuindo, para que aumente os meus esforços no sentido de não perdê-lo.

Ainda hoje, um dos principais objetivos da Matemática é ajudar o homem a contar. Ainda que as contas a serem feitas hoje sejam cada vez mais complexas, no fundo, no fundo, não passam de contagens.

Vamos exemplificar.... 

O salário mínimo aumentou 8,84% a partir de 01 de janeiro de 2015. Se eu ganho salário mínimo, para quanto foi o meu salário?

Bem, eu posso esperar receber para saber, eu posso assistir televisão para me informar, mas eu posso ser enganado por esses meios. O melhor mesmo é eu fazer as contas e ver quanto será o meu novo salário.

Para fazer essa conta eu preciso saber operacionalizar com os números decimais: dividir, multiplicar, subtrair e somar.

Rapidamente, eu posso pegar a minha calculadora e fazer as contas necessárias. Mas vamos observar uma coisa...

Todas as perguntas sobre divisão, multiplicação, subtração e adição estão na Tabuada. E, quase todas as explicações sobre como fazer as contas estão nos livros de Matemática, que temos aos milhares por aí.

Então, se eu posso contar com calculadoras, computadores, tabuadas e inúmeros livros, além da internet para saber as respostas de minhas contas, o que eu estou fazendo na escola?

Veja que não há razão para estar na escola estudando Matemática, se não for para aprender a fazer as contas que eu preciso, sem estar totalmente dependente das máquinas, dos livros e dos outros.

Só há razão para estar nas aulas de Matemática se eu mesmo quero fazer as contas e não apenas por a calculadora para fazê-las para mim. Só há razão para estudar se eu quiser explicar como se faz determinadas contas por mim mesmo, ao invés de apenas ler as explicações daqueles que sabem fazê-las e que escreveram os livros e os artigos que estão na internet.

Você quer mesmo aprender Matemática ou qualquer outra coisa na vida?

Juracy Farias Campos e Izaias Resplandes de Sousa. Ponte sobre o Rio Paraíso, em Paraíso do Leste, Poxoréu, MT, 1983.

Eu sou professor de Matemática e quero te ensinar a aprender Matemática, para que você seja autônomo, dono de suas respostas e explicações, para que você faça as suas próprias contas. Eu só preciso que você queira aprender. E para motivá-lo, eu quero dizer que tudo o que aprendemos em Matemática tem o objetivo de ajudar-nos a fazer as contagens que temos necessidade de fazer, para resolver os nossos problemas pela vida afora.

Vamos resolver o nosso problema inicial. Antes de iniciar a resolução de qualquer problema eu preciso fazer um levantamento dos dados que eu possuo.

Então vejamos...

Qual é o valor do salário mínimo que foi aumentado em 8,84%?

A resposta não cai do céu. É preciso pesquisar. A internet pode ajudar. Então, digite no seu programa de busca: "salário mínimo 2015". Dentre as opções disponibilizadas, clique em:

Salários Mínimos de 1995 a 2015 - Portal Contábeis
www.contabeis.com.br/tabelas/salario-minimo/



Salários Mínimos de 1995 a 2015. Ano, Vigência, Valor, Ato Legal, Percentual de aumento. 2015, 01/01/2015, R$ 788,00, Decreto 8.381/2014, 8,84 %.

Aí você terá acesso a essa tabela de Salários Mínimos de 1995 a 2015. E aí você já tem a resposta à sua pergunta. Foi fácil, não!

Salários Mínimos de 1995 a 2015

Ano	Vigência	Valor	Ato Legal	Percentual de aumento
2015	01/01/2015	R$ 788,00	Decreto 8.381/2014	8,84 %
2014	01/01/2014	R$ 724,00	Decreto 8.166/2013	6,78 %
2013	01/01/2013	R$ 678,00	Decreto 7.872/2012	9,00 %
2012	01/01/2012	R$ 622,00	Decreto 7.655/2011	14,13 %
2011	01/03/2011	R$ 545,00	Lei 12.382/2011	0,93 %
2011	01/01/2011	R$ 540,00	MP 516/2010	5,88 %
2010	01/01/2010	R$ 510,00	Lei 12.255/2010	9,68 %
2009	01/02/2009	R$ 465,00	Lei 11.944/2009	12,05 %
2008	01/03/2008	R$ 415,00	Lei 11.709/2008	9,21 %
2007	01/04/2007	R$ 380,00	Lei 11.498/2007	8,57 %
2006	01/04/2006	R$ 350,00	Lei 11.321/2006	16,67 %
2005	01/05/2005	R$ 300,00	Lei 11.164/2005	15,38 %
2004	01/05/2004	R$ 260,00	Lei 10.888/2004	8,33 %
2003	01/04/2003	R$ 240,00	Lei 10.699/2003	20,00 %
2002	01/04/2002	R$ 200,00	Lei 10.525/2002	11,11 %
2001	01/04/2001	R$ 180,00	MP 2.194-6/2001	19,21 %
2000	03/04/2000	R$ 151,00	Lei 9.971/2000	11,03 %
1999	01/05/1999	R$ 136,00	Lei 9.971/2000	4,62 %
1998	01/05/1998	R$ 130,00	Lei 9.971/2000	8,33 %
1997	01/05/1997	R$ 120,00	Lei 9.971/2000	7,14 %
1996	01/05/1996	R$ 112,00	Lei 9.971/2000	12,00 %
1995	01/05/1995	R$ 100,00	Lei 9.032/1995	42,86 %
1994	01/09/1994	R$ 70,00	MP 598/1994	8,04 %
1994	01/07/1994	R$ 64,79	Lei 8.880/1994	-

Agora você já sabe que o salário mínimo era R$ 724,00 e, com o aumento de 8,84% passou para R$ 788,00 a partir de 01 de janeiro de 2015.

Mas você aprendeu a fazer as contas para dizer que o valor está correto? Não aprendeu! Essa simples pesquisa respondeu ao que você queria saber, mas não te ensinou a fazer as contas para saber se a resposta está correta. Para aprender isso, você precisa aprender Matemática.

Dentre as várias maneiras de fazer essas contas, vejamos uma delas:

Pegue o valor do salário mínimo antigo (724,00), multiplique pelo índice de aumento (8,84), divida por 100 (já que o aumento é de 8,84 por CENTO; um cento é 100). O resultado é o valor do aumento. Some-o com os 724,00 e você terá o novo salário mínimo de R$ 788,00.

Nessa conta eu tenho 4 casas decimais (casas depois da vírgula). 2 zeros depois de 724 (em 724,00) e 84 (depois de 8,84). São 4 casas. Então eu devo colocar a vírgula no resultado da conta, antes de 4 casas, contadas da direita para a esquerda. Assim, como o resultado foi 64001600, vamos colocar a vírgula antes de 1600. De forma que o resultado da conta será 6400,1600. Esses dois zeros do final da conta podem ser cortado porque não valem nada. Assim o resultado será 6400,16.

Para dividir 6400,16 por 100 basta andar com a vírgula duas casas para a esquerda. Essa é a maneira mais simples de fazer a divisão por 100. Se fosse para dividir por 10, andaríamos uma casa para a esquerda, por 100 andamos duas casas, por mil seriam 3 casas e assim por diante. Para multiplicar por 10, 100 ou 1000 é só fazer o contrário, ou seja, andar com a vírgula para a direita, uma, 2 ou 3 casas e assim por diante. É fácil, não!

Então 6400,16 dividido por 100 deu 64,0016. Esse é o valor do aumento salarial. Como isso é dinheiro, é REAL (R$), nós somente consideraremos 2 casas decimais (depois da vírgula). Mas para fazer isso corretamente, não basta somente cortar as outras casas. Devemos seguir as regras de aproximação.

A última casa decimal do número 6400,0016 é 6, que é maior que 5. Então eu abandono esse 6 e aumento uma unidade no valor anterior 1, o qual passa a ser 2. Agora o número ficou 6400.002. Como o último dígito é 2 (que é menor que 5), simplesmente abandonamos essa casa. Aí o resultado fica 64,00. Esse é o valor do aumento, o qual, somando com 724,00 chega-se aos R$ 788,00 que é o valor do novo salário mínimo.

Ah, sim. Na hora de somar, coloque vírgula debaixo de vírgula. Não tem erro!

Essa é a Quedimar, responsável pela Merenda Escolar no período vespertino da EE. Pe. César Albisetti. Todas as tardes ela tem que calcular o percentual de merenda a mais ou a menos em relação ao dia anterior, que ela terá que fazer. Ela pode usar a calculadora para andar mais rápido, mas como profissional, também deverá saber fazer essas contas "no papel", como costumamos dizer.

Achou difícil. Parece que é mais difícil explicar o que fazer, do que realmente fazer as contas. O que você achou? 

Então é isso. Agora poderemos treinar um pouco, realizando operações decimais como essas.

Por que estudar funções?

Prof. Izaias Resplandes

Função é um caso particular de relação entre os elementos de dois conjuntos A e B em que cada elemento do conjunto A se relaciona com um e somente um elemento do conjunto B. 

Dizemos que é um caso particular, porque nem todas as relações são funções, mas apenas aquelas relações que se enquadram na definição acima. Exemplo:

Exemplo de função. Ao chegar em um posto de combustível para abastecer o carro, o motorista diz para o frentista: “ponha gasolina” e pergunta: “quanto eu pago?” Então o frentista redargue: “quantos litros?”. Se for 1 litro será R$ 3,65; se for 10 litros será R$ 36,50; se for 100 litros será R$ 365,00 e assim por diante. Ou seja, o valor “y” a ser pago pelo abastecimento vai depender da quantidade “x” de litros de gasolina abastecida. O valor “y” é obtido em função do valor “x” definido pelo sujeito . Essa função poderia ser definida pela seguinte regra:  y = 3,65 . x ou f(x) = 3,65 . x, já que y = f(x), isto é, y é função de x.

Créditos: http://professormarcianodantas.blogspot.com.br/2014/03/novas-relacoes-de-trabalho-nos-espacos.html

É de ver que tudo que existe nesse mundo está interligado e a maioria do aprendizado de algo novo se dá em função de um aprendizado já consolidado.

Créditos: https://demodelando.wordpress.com/tag/seletivos/

Dessa forma, uma das finalidades do estudo das funções é nos ajudar a compreender isso. Assim será o estudo da Matemática: partiremos das coisas que já sabemos para aquelas que pretendemos saber.

Créditos: http://dizendo.com.br/refletindo-sobre-disturbio-de-aprendizagem/

Na maioria das vezes, as nossas dificuldades de aprender alguma coisa decorre do fato de não termos aprendido outras. A saída mais rápida dessa crise é aprender aquelas coisas. E nós somos capazes de aprender, se desejarmos. Mas apenas se desejarmos.

Créditos: http://www.acasacuca.com.br/tag/reforco-escolar/

Segundo o prof. Amaral Fontoura, "aprendemos aquilo que nos interessa; o resto, decoramos para passar nos exames e esquecemos no dia seguinte".

Amaral Fontoura

Ao dizermos que tudo está interligado, poderíamos dizer que as nossas dificuldades de aprendizagem tenham alguma coisa a ver com a crise econômica do país?

A resposta é sim. Tudo tem a ver com tudo. Se o país está em crise econômica, certamente não investe no social e assim, o povo passa por privações. Falta alimento, moradia, saúde, etc.

Segundo a Teoria das Necessidades de Maslow (http://pt.wikipedia.org/wiki/Abraham_Maslow), a educação é uma necessidade que somente é perseguida pelo homem quando atende outras mais básicas. 

Abraham Harold Maslow

Para ele, as necessidades fisiológicas precisam ser saciadas para que se precise saciar as necessidades de segurança. Estas, se saciadas, abrem campo para as necessidades sociais, que se saciadas, abrem espaço para as necessidades de auto-estima. Se uma destas necessidades não está saciada, há a incongruência.

Disponível em: http://pt.wikipedia.org/wiki/Abraham_Maslow. Acesso em: 13 fev. 2015. 

Capra

De forma que tudo está interligado. O filme, "o ponto de mutação", que pode ser visto em: 

https://www.youtube.com/watch?v=tQlOIa80w5Y

é uma excelente pedida para que possamos compreender melhor essa interligação das coisas.

O livro de Capra

E se alguém tiver mais tempo ainda, também poderá ler o livro de mesmo título "O ponto de Mutação", de Fritjof Capra. Uma análise, tanto do livro, quanto do filme pode ser apreciada em:
http://metodologiacientfica.blogspot.com.br/2011/06/link-do-livro-o-ponto-de-mutacao.html

O filme baseado na obra de Capra

Então é isso.

Plano do Curso de Matemática para 2015

Um Plano de Curso de Matemática para o Ensino Médio/2015

Prof. Izaias Resplandes de Sousa

Carga horária: 3 aulas semanais.

Introdução

São eixos cognitivos para o Ensino Médio:

I- Dominar a norma culta da Língua Portuguesa e fazer uso das linguagens matemática, artística e científica.

II- Construir e aplicar conceitos das várias áreas do conhecimento para a compreensão de fenômenos naturais, de processos histórico-geográficos, da produção tecnológica e das manifestações artísticas.

III- Selecionar, organizar, relacionar, interpretar dados e informações representadas de diferentes formas, para tomar decisões e enfrentar situações-problema.

IV- Relacionar informações, representadas em diferentes formas, e conhecimentos disponíveis em situações concretas, para construir argumentação consistente.

V- Recorrer aos conhecimentos desenvolvidos para elaboração de propostas de intervenção solidária na realidade, respeitando os valores humanos e considerando a diversidade sociocultural.

De acordo com os PCN+, a área de Ciências da Natureza, Matemática e suas Tecnologias elegeu três grandes competências como metas a serem perseguidas:

1) Representação e comunicação: leitura, transmissão de idéias, interpretação e produção de textos nas diversas formas características da área.

Algumas habilidades referentes a esta competência são:

• Ler e interpretar dados apresentados em tabelas, gráficos, diagramas, fórmulas, equações, ou representações geométricas;

• Traduzir informações de uma dessas formas de apresentação para outra; utilizar essas formas de apresentação de informações selecionando, em cada caso, as mais adequadas;

• Ler e interpretar diferentes tipos de textos com informações apresentadas na forma de linguagem matemática como, por exemplo, artigos de conteúdo econômico, que aparecem em jornais e revistas, social ou cultural, em propagandas de promoções e vendas, apresentados em folhetos ou na mídia;

• Expressar-se com clareza sobre temas matemáticos oralmente ou por escrito.

2) Investigação e compreensão: capacidade de enfrentar desafios e resolução de situações problema, utilizando-se de conceitos e procedimentos peculiares (experimentação, abstração, modelagem).

Algumas habilidades referentes a esta competência são:

* Identificar os dados relevantes numa situação-problema para buscar possíveis resoluções;

* Elaborar estratégias para enfrentar e resolver uma dada situação-problema;

* Identificar regularidade em dadas situações; Fazer estimativas;

* Interpretar, fazer uso e elaborar modelos e representações matemáticas para analisar situações;

* Reconhecer relações entre a matemática e outras áreas do conhecimento.

3) Contextualização: no âmbito histórico ou sócio-cultural, na forma de análise crítica das idéias e dos recursos da área, para questionar, modificar ou resolver problemas propostos.

Algumas habilidades referentes a esta competência são:

• Compreender a construção do conhecimento matemático como um processo histórico, em estreita relação com as condições sociais, políticas e econômicas de uma determinada época;

• Compreender a responsabilidade social associada à aquisição e ao uso do conhecimento matemático, sentindo-se mobilizado para diferentes ações que envolvam seu interesse como cidadão ou de sua comunidade;

• Utilizar as ferramentas matemáticas para analisar situações de seu entorno real e propor soluções; etc.

Conteúdos Programáticos:

1º ano:

1º bimestre

Conteúdos.

Revisão de Produtos notáveis, fatoração, equações do 1º e 2º graus.

Objetivo específico:

- Recordar conhecimentos considerados como pré-requisitos necessários para os estudos de matemática no ensino médio.

- Reconhecer e determinar o quadrado da soma de dois termos;

- Reconhecer e determinar o quadrado da diferença entre dois termos;

- Reconhecer e determinar o produto da soma pela diferença de dois termos;

- Resolver situações-problema envolvendo produtos notáveis;

- Conhecer e aplicar os principais casos de fatoração

- Reconhecer uma equação do 1º grau e determine suas raízes;

- Interpretar e representar equações do 1º grau algébrica e geometricamente;

- Resolver situações-problema envolvendo equações do 1º grau;

- Reconhecer uma equação do 2º grau e determine suas raízes;

- Interpretar e representar equações do 2º grau algébrica e geometricamente;

- Resolver situações-problema envolvendo equações do 2º grau;

Conteúdos.

Plano cartesiano: teoria e aplicação.

Função: generalidades: conceito, notação, representação, domínio, contradomínio, imagem, gráfico. Função do 1º grau: Definição; Tipos (constante, afim, linear), coeficientes angular e linear, zero da função, crescimento e decrescimento, estudo do sinal, construção, leitura e análise de gráficos.

Objetivos específicos:

- Identificar e construir o plano cartesiano.

- Representar pontos no plano cartesiano.

- Formalizar o conceito de função.

- Reconhecer funções em situações do cotidiano.

- Reconhecer domínio, imagem e contradomínio da função.

- Determinar a imagem pela lei y = f(x);

- Estudar o sinal da função.

- Representar uma função por meio de diagramas.

- Representar uma função por meio de gráficos.

- Reconhecer uma função pela análise gráfica.

- Reconhecer o gráfico das funções afim, linear e constante.

- Construir o gráfico das funções afim, linear e constante.

- Determinar a lei de associação, com base no gráfico das funções afim, linear e constante.

- Estudar os sinais dos períodos das funções afim e linear

  

2º bimestre.

Conteúdos.

Função quadrática: definição, zero da função; Vértice da parábola; Imagem; Construção do gráfico

Objetivos específicos:
- Identificar a lei de formação de uma função quadrática a partir de sua representação algébrica e/ou gráfica;

-  Reconhecer uma função quadrática nas suas representações algébrica e gráfica;

- Calcular as raízes de uma função quadrática;

- Identificar o ponto de máximo e de mínimo de uma função quadrática;

- Definir o vértice da parábola na função quadrática

- Construir o gráfico da função quadrática

- Determinar o número de raízes de uma função quadrática por meio da análise de sua representação gráfica (concavidade da parábola);

- Identificar uma função quadrática em situações descritas em um texto, representando-a algébrica e/ou graficamente;

- Resolver situações-problema que envolvam a função quadrática;

  

3º bimestre.

Conteúdos.

Sequências Numéricas. Termo geral. Progressão Aritimética: definição, classificação, termo geral, Resolução de problemas, Soma dos termos da PA. Progressão Geométrica: definição, classificação, termo geral, Resolução de problemas, Soma dos termos da PG.

Objetivos específicos:

- Diferenciar os conceitos de sequência e conjunto.

- Identificar a lei de formação de Progressões Aritméticas;

- Determinar os termos de uma sequência, a partir de sua lei de formação.

- Definir uma progressão aritmética.

- Classificar uma progressão aritmética como crescente, decrescente ou constante.

- Compreender e operar com a fórmula do termo geral de uma Progressão Aritmética;

- Determinar, utilizando a lei de formação, um termo qualquer de uma progressão aritmética.

- Representar genericamente uma PA.

- Calcular a soma dos n primeiros termos de uma PA.

- Compreender e operar com a fórmula da soma dos termos de uma Progressão Aritmética;

- Definir uma progressão geométrica (PG).

- Identificar a lei de formação de Progressões Geométricas;

-  Identificar a razão de uma Progressão Geométrica;

- Classificar uma PG como crescente, decrescente, constante, alternante ou quase nula.

- Determinar, utilizando a lei de formação, um termo qualquer de uma PG.

-  Compreender e operar com a fórmula da soma dos termos de uma Progressão Geométrica;

- Representar genericamente uma PG.

- Calcular a soma dos n primeiros termos de uma PG.

-  Identificar uma Progressão Geométrica em situações descritas em um texto, representando-a em linguagem algébrica;

-  Resolver situações-problema envolvendo Progressões Aritméticas e/ou Geométricas;

4º bimestre

Conteúdos.

Triângulo retângulo. Relações métricas. Trigonometria no triângulo retângulo. Seno, Cosseno e Tangente de um ângulo agudo.

Objetivos específicos:

- Identificar as relações métricas no triângulo retângulo e aplicá-las na resolução de problemas variados.

- Calcular a medida de um lado de um triângulo, a partir das medidas de outro lado e de um ângulo agudo desse triângulo.
-  Resolver situações-problema envolvendo as relações métricas no triângulo retângulo;

- Compreender os conceitos e calcular os valores aproximados do seno, cosseno e tangente de um ângulo agudo de um triângulo retângulo.

-  Utilizar as razões trigonométricas no triângulo retângulo para obter relações entre ângulos e lados na determinação de suas medidas;

-  Resolver situações-problema envolvendo as relações trigonométricas no triângulo retângulo;

2º ano:

1º bimestre.

Conteúdos:

Matrizes: introdução, representação, tipos de matrizes, Igualdade de matrizes. Adição, subtração e multiplicação de matrizes.

Objetivos específicos:

- Conceituar e interpretar matrizes e suas operações;

- Reconhecer, interpretar e transcrever dados em linguagem matricial;

-Reconhecer uma matriz e saber utilizar suas operações.

- Classificar as matrizes em identidade, nula, transposta, oposta, linha, coluna, quadrada.

- Resolver situações-problema envolvendo a igualdade e operações de adição, subtração e multiplicação de matrizes;

  

2º bimestre.

Conteúdos:

Determinantes: conceito; Cálculo de determinantes pela Regra de Sarrus, Regra de Cramer e Teorema de Laplace.

 Objetivos específicos:

- Calcular o determinante de matrizes de ordem 1, 2 e 3

- Conhecer e aplicar a Regra de Sarrus, a Regra de Cramer e o Teorema de Laplace no cálculo de determinantes.

  

3º bimestre.

Conteúdos:

Sistemas Lineares: métodos de resolução: adição, substituição, escalonamento. Discussão de um sistema.

 Objetivos específicos:

- Reconhecer uma equação linear.

- Resolver problemas que envolvam sistemas de equações lineares.

- Reconhecer uma equação linear.

- Determinar soluções de uma equação linear possível.

- Classificar uma equação linear em possível ou

impossível.

- Classificar os sistemas lineares em SPD, SPI e SI

- Resolver sistemas lineares pelos métodos da adição e substituição

  

4º bimestre.

Conteúdos:

Análise combinatória: Princípio fundamental da contagem. Fatorial de um número natural. Agrupamentos simples. Permutações. Arranjos. Combinações. Permutações de elementos repetidos.

Objetivos específicos:

- Reconhecer situações em que a contagem dos resultados possíveis é parte da resolução do problema.

- Definir o que é Análise combinatória.
- Aplicar o princípio fundamental de contagem.

- Calcular o fatorial de um número natural.

- Resolver equações envolvendo fatoriais

- Classificar agrupamentos simples como arranjos ou combinações.

- Reconhecer um arranjo simples.

- Construir os arranjos simples formados por p elementos escolhidos entre n elementos distintos.

- Calcular o número de arranjos simples de n elementos tomados p a p.

- Reconhecer uma permutação simples.

- Construir permutações de n elementos distintos.

- Calcular o número de permutações simples e de permutações com elementos repetidos.

- Reconhecer uma combinação simples.

- Construir as combinações simples formadas por p elementos escolhidos entre n elementos distintos.

- Relacionar os números Cn,p e Anp.

Conteúdos:

Probabilidade: espaço amostral, evento, freqüência relativa e probabilidade. Aplicações.

Objetivos específicos:

- Determinar o espaço amostral de um experimento aleatório.

- Determinar o número de elementos de um espaço amostral.

- Definir evento de um espaço amostral.

- Calcular a probabilidade de ocorrer um evento em um espaço amostral.

- Reconhecer eventos complementares.

- Aplicar as propriedades das probabilidades.

- Resolver problemas de probabilidade

3º ano:

1º bimestre.

Conteúdos:

Atividades de revisão de funções: domínio, imagem, valor numérico, gráficos,  diagramas, leis de formação, tipos de função: constante, 1º grau, 2º grau, crescente, decrescente, quadrática Subconjuntos dos Reais. Linguagem matemática

Objetivos específicos:

- Rever conteúdos do 1º ano médio, considerados pré-requisitos para o prosseguimento dos estudos.

Conteúdos:

Estatística: tabelas de freqüência, representações gráficas, Medidas de tendência central. Medidas de dispersão.

Objetivos específicos:

- Conceituar Estatística

- Conceituar população, amostra, frequência e frequência relativa.

- Separar uma amostra de números em classes.

- Construir tabelas de distribuição de frequência.

- Analisar, interpretar e organizar dados e informações de pesquisas estatísticas em gráficos e tabelas

- Representar uma distribuição de frequência em gráfico de linha, gráfi co de barras (horizontais e verticais) e gráfico de setores.

- Construir e interpretar histogramas de uma distribuição de frequência de classes não unitárias.

- Conceituar média aritmética.

- Conceituar média ponderada.

- Conceituar moda e mediana.

- Conceituar as medidas de dispersão: Variância e Desvio Padrão

- Calcular a Variância

- Calcular o desvio padrão

- Analisar e interpretar resultados de pesquisas estatísticas realizadas por amostragem;

- Identificar e interpretar dados e informações estatísticas por meio de sua representação gráfica;

- Resolver situações-problema envolvendo pesquisas estatísticas.

  

2º bimestre.

Conteúdos:

Números complexos: introdução. Forma algébrica de z. Conjugado. Número complexo. Operações em z.

Objetivos específicos:

- Identificar os diferentes conjuntos numéricos e as propriedades inerentes a cada um deles;

- Introduzir a noção de números complexos.

- Identificar a unidade imaginária (i) como elemento do conjunto dos números complexos

- Conceituar número complexo e representá-lo na forma algébrica e gráfica.

- Operar com a forma algébrica dos números complexos

- Calcular potências de expoente inteiro de i e de números complexos na forma a + bi, sendo a e b números reais.

- Resolver situações-problema envolvendo o cálculo de equações cujas raízes não são reais;

  

3º bimestre.

Conteúdos:

Geometria Analítica: Ponto: distância entre dois pontos. Ponto médio de um segmento. Mediana e baricentro. Condição de alinhamento de 3 pontos. Resolução de problemas.

Objetivos específicos:

- Conhecer a origem do sistema de coordenadas cartesianas.

- Calcular a distância entre dois pontos.

- Obter o ponto médio de um segmento de reta.

- Identificar, graficamente, a inclinação de uma reta no plano cartesiano.

- Calcular o coeficiente angular de uma reta não vertical, conhecendo sua inclinação ou as coordenadas de dois de seus pontos.

- Verificar se três pontos do plano cartesiano são ou não colineares.

  

4º bimestre.

Conteúdos:

A reta: equação geral da reta. Intersecção de retas. Inclinação de uma reta (coeficiente angular). Equação reduzida. Paralelismo. Perpendicularidade.

Objetivos específicos:

- Representar uma reta do plano cartesiano por meio de uma equação geral.

- Determinar os pontos de intersecção de duas retas concorrentes.

- Expressar a equação geral de uma reta não vertical na forma reduzida, destacando os coeficientes angular e linear.

- Reconhecer a posição relativa de duas retas não verticais a partir de seus coeficientes angulares

 Metodologia:  Aulas expositivas e trabalhos individuais e em grupo. Excepcionalmente, conforme a disponibilidade será utilizada os recursos da mídia e informática.

Avaliação: Conforme as normas da escola.